Summary
Quantum computers won’t politely wait for our defenses to catch up. The race to build post-quantum cryptography is full of ideas, drawn from deep corners of mathematics, and history shows plenty of them don’t survive first contact with real attacks.
A few contenders still stand strong, but none are beyond doubt.
That’s why we need to pay attention now. The field is in motion, and while NIST’s standardized algorithms are today’s best bet, the real key is agility: being ready to shift as new breakthroughs emerge.
In this blog, we’ll look at the leading approaches and the security foundations they rely on, to see where confidence is justified and where caution is wiser.
Table of content
Quantum code breaking? You’d get further with an 8-bit computer, an abacus, and a dog.
— Peter Gutmann, Why Quantum Cryptanalysis is Bollocks (2025) [1]
Breaking it down
Most widely used public-key (asymmetric) algorithms rely on the difficulty of one of three mathematical problems: the integer factorization problem, the discrete logarithm problem or the elliptic-curve discrete logarithm problem.
All of these problems can theoretically feasibly be solved on a sufficiently powerful quantum computer running Shor’s algorithm or possibly alternatives. Current symmetric cryptographic algorithms and hash functions do not suffer the same problem. Therefore, we focus exclusively on asymmetric cryptography here.
A great machine shall arise, and it will cast aside all existing cryptography, there shall be Famine, Plague, War, and a long arable field.
— Peter Gutmann
As of 2025, no sufficiently powerful quantum computers exist[2] or are even in sight[3]. ‘Harvest now, decrypt later’ collection is plausible, which justifies beginning measured migration planning. Post‑quantum (also called ‘quantum-safe’) cryptography has therefore received sustained attention over the past decades. (Symmetric ciphers and hash functions are not “broken” by quantum computing and Grover’s algorithm merely suggests larger key/output sizes.)
Growing venture investment and optimistic marketing narratives have added some hype around post‑quantum cryptography, while practical work proceeds in a measured, standards‑guided way.
Here Be No Dragons
Inevitably, some mathematical notions (or even phrases) occur in texts describing mathematical concepts. Sorry about that.
Here’s Euler’s formula, that serves no purpose here other than to encourage reading on since it’s the last and only actual formula in this document. Promised.
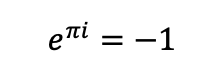
Approach Directions
The following alternative approaches are pursued in the context of creating asymmetric cryptographic algorithms intended to be quantum resilient.
Lattice-based cryptography
Under the assumption that a class of known problems from the field of lattice theory [4] cannot be solved efficiently, constructing cryptographic primitives involving lattices in their construction or the proof of security is meant to achieve resiliency against quantum computing approaches.
Examples are Ring-LWE (RLWE) based algorithms, and the CRYSTALS-Kyber and CRYSTALS-Dilithium algorithms in the Module-Lattice-Based Digital Signature Standard as announced by NIST in 2024.
A useful way to picture the underlying problem, the Shortest Vector Problem (SVP), is to imagine walking in strange boots. Normal boots might let you take a single step north or east. These cryptographic boots, however, might force you into bizarre leaps — like a million steps north-north-east, or twenty steps north-east. The challenge is finding the absolute shortest path possible given all the strange moves you’re allowed. Cryptography counts on the fact that, even knowing the rules, this is monstrously difficult to solve.
Isogeny-based cryptography
Isogeny-based cryptographic systems rely on the properties of supersingular isogeny graphs, that have vertices representing supersingular elliptic curves over finite fields and edges representing isogenies between curves.
Known instances are:
- SQIsign, a signature scheme based on the categorical equivalence [5] between supersingular elliptic curves and maximal orders in particular types of quaternion algebras, and
- CSIDH, a Diffie–Hellman-like key exchange intended to serve as a straightforward quantum-resistant replacement for the currently widely used Diffie–Hellman and elliptic curve Diffie–Hellman key-exchange methods.
A widely noticed isogeny-based construction, SIDH/SIKE, was spectacularly broken in 2022. That particular attack is specific to SIDH/SIKE though, and has no generalizations to other isogeny-based approaches.
Hash-based cryptography
In hash-based signature schemes, one-time signature schemes are used as building blocks, using structures like Lamport signatures, Merkle trees and similar to extend beyond the one-time usage limit. Note that this implies statefulness, which complicates implementation and operationalization.
Any hash function satisfying security assumptions can be used, and if one such hash function used turns out flawed it can be replaced, effectively producing a corresponding new instantiation.
NIST incorporated stateful hash-based cryptography in its proposed standards in 2019, based on the eXtended Merkle Signature Scheme (XMSS), the Stateless Hash-Based Digital Signature Standard (SPHINCS+), and Leighton–Micali Signatures (LMS).
Code-based cryptography
Code-based cryptography is based on error-correcting codes, such as the McEliece and Niederreiter encryption algorithms and the related Courtois, Finiasz and Sendrier Signature schemes. The original McEliece approach, using random Goppa codes, has withstood scrutiny for over four decades. However, that approach involves unwieldy key sizes, and variants trying to pack more structure into the code to reduce key sizes turned out to be insecure.
The EU’s Post-Quantum Cryptography Study Group has proposed [6] the Classic McEliece public key encryption system for long-term quantum resilience. Other proposed algorithms are HQC, BIKE.
Multivariate cryptography
Solving systems of multivariate polynomial equations is a known hard problem; it’s proven to be NP-complete[7]. Cryptographic algorithms based on it have a near four decades history.
While many of the early proposals have since been shown to be flawed (and, hence, broken), the Lifted Unbalanced Oil and Vinegar (LUOV), GeMMS, Rainbow, and MQDSS multivariate cryptography signature schemes were incorporated in NIST’s second round PQC standardization process[8].
Security Reductions
When proving the equivalence of a cryptographic algorithm and a known hard mathematical problem, this effectively implies that cracking the algorithm is as hard as solving that mathematical problem. This proof strategy is called reduction, and it is prevalent in cryptography, complexity theory, and many other fields of mathematics.
A number of security reductions have been established.
Lattice-based cryptography • RLWE-SIG
RLWE-SIGl, at least some versions of it, are reducible to the shortest-vector problem (SVP), which is a known NP-hard[9] problem.
Hash-based cryptography • Merkle Signature Scheme
Merkle Hash Tree security is provably reducible to the underlying hash function’s security.
Code-based cryptography • McEliece
There is a security reduction for the McEliece Encryption System to the syndrome decoding problem (SDP), which is a known NP-hard problem.
Multivariate cryptography • Unbalanced Oil and Vinegar
Unbalanced Oil and Vinegar signature schemes are asymmetric cryptographic primitives based on multivariate polynomials over a finite field. There is a reduction of generic multivariate quadratic UOV systems to the NP-hard multivariate quadratic equation solving problem.
Standardization Efforts and Bodies
Standardization bodies are currently in a flux. The International Organization for Standardization (ISO) is in the process of evaluating candidates and electing approved algorithm applications. The United States National Institute of Standards and Technology (NIST) that gets to define federal standards (FIPS) for the US is also of some historical relevance still.
The following table shows the current state of affairs.
| Algorithm | Type | ISO | NIST |
| Frodo-KEM | Lattice-based, Learning With Error | In Process | Other Alternative |
| CRYSTALS-Kyber (FIPS-203) | Lattice-based, ML-KEM: Module Learning w/Error | In process | Main |
| Classic McEliece | Code-based: goppa codes | Being Standardised | No |
| BIKE | Code-based | No | No |
| HQC | Code-based | In Process | Standard |
| NTRU | Lattice-based cryptography | In Process | No |
| CRYSTALS-Dilithium (FIPS-204) | ML-DSA: Module Short Integer Solution | In Process | Standard |
| Falcon (FIPS-204) | FN-DSA: Short Integer Solution | In Process | Standard |
| SPHINCS+ (FIPS-205) | SLH-DSA:[83] hash based | In Process | Standard |
| XMSS | hash-based | Being Standardised | Approved |
Evaluation
The body of proposed PQC algorithms is vast, and is rooted in multiple fields of advanced mathematics. In the (roughly) half century, many approaches and implementations have been examined, tried and tested; and, as is par for the course in these matters, many approaches (or optimizations to make solid, but somehow cumbersome ones less impractical) crashed and burned.
Some approaches remain standing, showing promise, notably lattice-based and certain code-based schemes, but they still need years of rigorous testing. Others have collapsed under clever attacks, reminding us that post-quantum cryptography is a living field, not settled science. For practitioners, the safe bet in 2025 is to follow NIST’s standardized algorithms while keeping systems cryptographically agile, ready to swap in new primitives as the landscape shifts.
[1] Peter Gutmann, “Why Quantum Cryptanalysis is Bollocks”, https://www.cs.auckland.ac.nz/~pgut001/pubs/bollocks.pdf; 2025.
[2] Bruce Schneier, “Cheating on Quantum Computing Benchmarks”, https://www.schneier.com/blog/archives/2025/07/cheating-on-quantum-computing-benchmarks.html; July 31 2025.
[3] Peter Gutmann & Stephan Neuhaus, “Replication of Quantum Factorisation Records with an 8-bit Home Computer, an Abacus, and a Dog”, IACR, https://eprint.iacr.org/2025/1237.pdf; March 2025.
[4] B.A. Davey, H.A. Priestley, “Introduction to Lattices and Order”, 2nd ed. Cambridge University Press; 2002.
[5] Saunders Mac Lane, “Categories for the Working Mathematician. Graduate Texts in Mathematics”, Vol. 5 (2nd ed.). Springer. ISBN 0-387-98403-8. Zbl 0906.18001; September 1998.
[6] Daniel Augot, Lejla Batina, Daniel J. Bernstein, Joppe Bos, Johannes Buchmann, Wouter Castryck, Orr Dunkelman, Tim Güneysu, Shay Gueron, Andreas Hülsing, Tanja Lange, Mohamed Saied Emam Mohamed, Christian Rechberger, Peter Schwabe, Nicolas Sendrier, Frederik Vercauteren, and Bo-Yin Yang, “Post-Quantum Cryptography for Long-Term Security”, http://pqcrypto.eu.org/docs/initial-recommendations.pdf; 7. September 2015.
[7] Michael R. Garey, David S. Johnson, “Computers and Intractability: a Guide to the Theory of NP-Completeness”, San Francisco: W.H. Freeman. ISBN 0-7167-1044-7. OCLC 4195125; 1979.
[8] NIST, “The 2nd Round of the NIST PQC Standardization Process”, https://csrc.nist.gov/Presentations/2019/the-2nd-round-of-the-nist-pqc-standardization-proc; 2019.
[9] Michael R. Garey, David S. Johnson, “Computers and Intractability: a Guide to the Theory of NP-Completeness”, San Francisco: W.H. Freeman. ISBN 0-7167-1044-7. OCLC 4195125; 1979.
FAQ
What is post-quantum cryptography (PQC)?
Post-quantum cryptography refers to cryptographic algorithms designed to withstand attacks from quantum computers. Unlike classical algorithms, which can be broken by Shor’s algorithm, PQC focuses on problems that remain hard even for quantum computers.
Why are today’s cryptographic systems at risk from quantum computing?
Most public-key algorithms, such as RSA and elliptic-curve cryptography, rely on mathematical problems like integer factorization and discrete logarithms. Quantum algorithms can solve these efficiently, making current systems vulnerable once large-scale quantum computers exist.
Which PQC approaches are considered most promising?
Lattice-based cryptography (e.g., CRYSTALS-Kyber and CRYSTALS-Dilithium) and certain code-based schemes (e.g., Classic McEliece) are considered leading candidates. They are part of the algorithms standardized by NIST for future use.
Are symmetric ciphers affected by quantum computers?
Symmetric algorithms and hash functions are less affected. Grover’s algorithm can speed up brute-force attacks, but doubling key sizes (e.g., from 128 to 256 bits) provides sufficient protection.
What should organizations do today to prepare for the quantum threat?
Organizations should start planning migrations to PQC algorithms, monitor NIST standards, and build cryptographic agility into their systems to quickly adopt new primitives as the field evolves.


