Leestijd: 10 minuten
Categorie: Post-Quantum Cryptography
Auteur: Jeroen Scheerder, Derk Bell
Samenvatting
Quantumcomputers gaan niet netjes wachten tot wij onze cybersecurity op orde hebben. De zoektocht naar post-quantumcryptografie zit vol slimme wiskundige ideeën, maar veel daarvan vallen om zodra ze serieus onder vuur komen te liggen.
Een paar blijven overeind, maar zekerheid is er nog lang niet.
Juist daarom moeten we er nú mee bezig zijn. De algoritmes die NIST heeft goedgekeurd zijn voorlopig de beste keuze, maar het belangrijkste is dat systemen flexibel blijven: zodat je makkelijk kunt schakelen als er weer iets nieuws opduikt.
In deze blog kijken we naar de belangrijkste aanpakken en de wiskunde erachter, en zie je waar je redelijk gerust op kunt zijn en waar je beter scherp blijft.
Inhoudsopgave
Quantum code breaking? You’d get further with an 8-bit computer, an abacus, and a dog.
— Peter Gutmann, Why Quantum Cryptanalysis is Bollocks (2025) [1]
De (wiskundige) basis
De meest gebruikte asymmetrische public-key algoritmes steunen op de moeilijkheid van drie wiskundige puzzels: het ontbinden van grote getallen in priemfactoren, het oplossen van discrete logaritmes, of de variant daarvan op elliptische krommen.
Een krachtige kwantumcomputer zou die puzzels in theorie kunnen kraken met Shor’s algoritme (of iets vergelijkbaars). Voor symmetrische algoritmes en hashfuncties geldt dit probleem niet. Daarom richten we ons hier uitsluitend op asymmetrische cryptografie.
A great machine shall arise, and it will cast aside all existing cryptography, there shall be Famine, Plague, War, and a long arable field.
— Peter Gutmann
Er zijn in 2025 nog geen kwantumcomputers krachtig genoeg om de huidige asymmetrische versleuteling te breken[2] en het lijkt onwaarschijnlijk dat dit op korte termijn in zicht komt[3]. Wel is het aannemelijk dat aanvallers nu al data verzamelen om die later, zodra het kan, te ontsleutelen: ‘Harvest now, decrypt later’. Daarom is het verstandig om alvast een migratieplan klaar te hebben. (Symmetrische versleuteling en hashfuncties lopen dit risico niet: die worden niet door kwantumcomputers gekraakt. Het algoritme van Grover wijst er alleen op dat grotere sleutels of uitvoergroottes nodig zijn om veilig te blijven.)
Door toenemende investeringen en optimistische marketingverhalen is er wel wat hype ontstaan rond post‑kwantumcryptografie. In de praktijk gaat de ontwikkeling echter rustig en zorgvuldig verder, geleid door duidelijke standaarden.
Here Be No Dragons
We hebben het over wiskundige concepten, en dat betekent dat er onvermijdelijk wat wiskundige termen langskomen (soms zelfs hele zinnen). Alvast onze excuses. Hieronder zie je de formule van Euler. Het enige doel daarvan is je te motiveren om door te lezen, want dit is de eerste én meteen de laatste formule die we in deze blog laten zien. Echt waar.
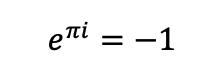
Verschillende aanpakken
Er worden verschillende methoden onderzocht om asymmetrische cryptografie te realiseren die bestand is tegen kwantumcomputers.
Lattice-based cryptografie
Het idee hier is dat bepaalde wiskundige problemen uit de zogenoemde lattice theory [4] niet efficiënt op te lossen zijn. Cryptografische systemen die hierop zijn gebaseerd gebruiken ‘lattices’ en bouwen hun security daarop.
Voorbeelden zijn algoritmes gebaseerd op Ring-LWE (RLWE) en de CRYSTALS-Kyber en CRYSTALS-Dilithium algoritmes in de Module-Lattice-Based Digital Signature Standard, zoals in 2024 door NIST aangekondigd.
Een makkelijke manier om het onderliggende probleem, het Shortest Vector Problem (SVP), voor te stellen, is door je voor te stellen dat je op vreemde laarzen loopt. Met gewone laarzen zet je één stap naar het noorden of naar het oosten. Deze cryptografische laarzen kunnen je echter rare sprongen laten maken – bijvoorbeeld een miljoen stappen naar noord-noord-oost, of twintig stappen naar noordoost. De uitdaging is om de kortst mogelijke route te vinden, gegeven al die rare sprongen. Cryptografie gaat ervan uit dat dit, zelfs als je de regels kent, ontzettend lastig is.
Isogeny-based cryptografie
Isogeny-gebaseerde cryptografische systemen gebruiken supersinguliere isogeniegrafieken. In deze grafieken staan de knopen voor supersinguliere krommen over eindige velden, en de verbindingen geven de isogenieën tussen die krommen weer.
Bekende voorbeelden zijn:
- SQIsign, een signature-schema gebaseerd op de verbanden tussen supersinguliere elliptische krommen en bepaalde quaternionele algebra’s, en
- CSIDH, een Diffie–Hellman-achtige methode voor sleuteluitwisseling, bedoeld als eenvoudige, kwantumbestendige vervanging van de standaard Diffie-Hellman en elliptische-kromme Diffie-Hellman methoden.
Een veelbesproken constructie, SIDH/SIKE, werd in 2022 op spectaculaire wijze gekraakt. Die aanval was echter specifiek voor SIDH/SIKE en geldt niet voor andere isogeny-gebaseerde systemen.
Hash-based cryptografie
Bij hash-gebaseerde handtekeningen worden eenmalige handtekeningen gebruikt als bouwstenen. Structuren zoals Lamport-signatures en Merkle-trees helpen om de eenmalige gebruikslimiet te omzeilen. Dit betekent dat er sprake is van impliciete statefulness, wat de implementatie en het gebruik ingewikkelder maakt.
Elke hashfunctie die aan de veiligheidsvereisten voldoet, kan gebruikt worden. Als zo’n hashfunctie later zwak blijkt, kan deze worden vervangen, waardoor er effectief een nieuwe versie van het systeem ontstaat.
In 2019 heeft NIST stateful hash-based cryptografie opgenomen in de voorgestelde normen, gebaseerd op het eXtended Merkle Signature Scheme (XMSS), de stateless SPHINCS+ en Leighton–Micali Signatures (LMS).
Code-based cryptografie
Code-gebaseerde cryptografie gebruikt foutcorrectiecodes, zoals de McEliece- en Niederreiter-algoritmes, en de gerelateerde handtekeningenschema’s van Courtois, Finiasz en Sendrier. De originele McEliece-aanpak, met willekeurige Goppa-codes, heeft al meer dan veertig jaar standgehouden.
Het nadeel is dat de sleutels erg groot zijn. Varianten die proberen de sleutels kleiner te maken door meer structuur in de codes te stoppen, bleken onveilig. De EU Post-Quantum Cryptography Study Group [6] heeft het Classic McEliece-systeem voorgesteld voor langdurige kwantumbestendigheid. Andere voorgestelde algoritmes zijn HQC en BIKE.
Multivariate cryptografie
Het oplossen van systemen van polynomiale vergelijkingen is een bekend moeilijk probleem; het is zelfs NP-complete[7]. Cryptografische algoritmes die hierop gebaseerd zijn, bestaan al bijna veertig jaar.
Veel vroege voorstellen bleken uiteindelijk onveilig, maar enkele multivariate handtekeningenschema’s, zoals Lifted Unbalanced Oil and Vinegar (LUOV), GeMMS, Rainbow en MQDSS, zijn opgenomen in de tweede ronde van het NIST-standaardisatieproces voor post-quantum cryptografie.[8].
Security Reducties
Als aangetoond wordt dat een cryptografisch algoritme equivalent is aan een bekend moeilijk probleem, betekent dat in feite dat het breken van het algoritme net zo lastig is als het oplossen van dat wiskundige probleem. Zo’n bewijsaanpak heet een reductie en wordt veel gebruikt in cryptografie, complexiteitstheorie en andere takken van de wiskunde.
Er zijn een aantal security reducties vastgesteld.
Lattice-based cryptografie • RLWE-SIG
Sommige versies van RLWE-SIG zijn herleidbaar tot het Shortest Vector Problem (SVP), een bekend NP-hard[9] probleem.
Hash-based cryptografie • Merkle Signature Scheme
De security van Merkle Hash Trees kan aangetoond worden op basis van de security van de onderliggende hashfunctie.
Code-based cryptografie • McEliece
Het McEliece Encryption System kan worden gereduceerd tot het decoding problem (SDP), een bekend NP-hard probleem.
Multivariate cryptografie • Unbalanced Oil and Vinegar
UOV-handtekeningenschema’s zijn gebaseerd op multivariate polynomen over een eindig veld. Generieke UOV-systemen zijn herleidbaar tot het NP-hard multivariate quadratic equations-probleem.
Standardization Efforts and Bodies
Standaardisatie-instanties zitten momenteel in een overgangsfase. De International Organization for Standardization (ISO) evalueert kandidaten en selecteert goedgekeurde algoritme-toepassingen. Ook het Amerikaanse National Institute of Standards and Technology (NIST), dat federale normen (FIPS) vaststelt, speelt nog steeds een belangrijke rol.
Onderstaande tabel laat de huidige stand van zaken zien.
| Algoritme | Type | ISO | NIST |
| Frodo-KEM | Lattice-based, Learning With Error | In Process | Other Alternative |
| CRYSTALS-Kyber (FIPS-203) | Lattice-based, ML-KEM: Module Learning w/Error | In process | Main |
| Classic McEliece | Code-based: goppa codes | Being Standardised | No |
| BIKE | Code-based | No | No |
| HQC | Code-based | In Process | Standard |
| NTRU | Lattice-based cryptography | In Process | No |
| CRYSTALS-Dilithium (FIPS-204) | ML-DSA: Module Short Integer Solution | In Process | Standard |
| Falcon (FIPS-204) | FN-DSA: Short Integer Solution | In Process | Standard |
| SPHINCS+ (FIPS-205) | SLH-DSA:[83] hash based | In Process | Standard |
| XMSS | hash-based | Being Standardised | Approved |
Evaluatie
Het aantal voorgestelde post-kwantumcryptografie-algoritmen is enorm en komt uit verschillende takken van de geavanceerde wiskunde. In de afgelopen vijftig jaar zijn veel benaderingen onderzocht, getest en beproefd. Zoals te verwachten, zijn veel pogingen – bijvoorbeeld om bestaande benaderingen praktischer te maken – uiteindelijk mislukt.
Sommige benaderingen blijven veelbelovend, vooral lattices en bepaalde code-gebaseerde schema’s, maar ze moeten nog jarenlang grondig getest worden. Andere zijn ten onder gegaan door slimme aanvallen, wat laat zien dat post-kwantumcryptografie een dynamisch vakgebied is, geen vaste wetenschap. Voor de praktijk betekent dit dat het in 2025 het slimst is om de door NIST gestandaardiseerde algoritmen te volgen en tegelijkertijd systemen flexibel te houden, zodat nieuwe primitives ingevoerd kunnen worden als het landschap verandert.
[1] Peter Gutmann, “Why Quantum Cryptanalysis is Bollocks”, https://www.cs.auckland.ac.nz/~pgut001/pubs/bollocks.pdf; 2025.
[2] Bruce Schneier, “Cheating on Quantum Computing Benchmarks”, https://www.schneier.com/blog/archives/2025/07/cheating-on-quantum-computing-benchmarks.html; July 31 2025.
[3] Peter Gutmann & Stephan Neuhaus, “Replication of Quantum Factorisation Records with an 8-bit Home Computer, an Abacus, and a Dog”, IACR, https://eprint.iacr.org/2025/1237.pdf; March 2025.
[4] B.A. Davey, H.A. Priestley, “Introduction to Lattices and Order”, 2nd ed. Cambridge University Press; 2002.
[5] Saunders Mac Lane, “Categories for the Working Mathematician. Graduate Texts in Mathematics”, Vol. 5 (2nd ed.). Springer. ISBN 0-387-98403-8. Zbl 0906.18001; September 1998.
[6] Daniel Augot, Lejla Batina, Daniel J. Bernstein, Joppe Bos, Johannes Buchmann, Wouter Castryck, Orr Dunkelman, Tim Güneysu, Shay Gueron, Andreas Hülsing, Tanja Lange, Mohamed Saied Emam Mohamed, Christian Rechberger, Peter Schwabe, Nicolas Sendrier, Frederik Vercauteren, and Bo-Yin Yang, “Post-Quantum Cryptography for Long-Term Security”, http://pqcrypto.eu.org/docs/initial-recommendations.pdf; 7. September 2015.
[7] Michael R. Garey, David S. Johnson, “Computers and Intractability: a Guide to the Theory of NP-Completeness”, San Francisco: W.H. Freeman. ISBN 0-7167-1044-7. OCLC 4195125; 1979.
[8] NIST, “The 2nd Round of the NIST PQC Standardization Process”, https://csrc.nist.gov/Presentations/2019/the-2nd-round-of-the-nist-pqc-standardization-proc; 2019.
[9] Michael R. Garey, David S. Johnson, “Computers and Intractability: a Guide to the Theory of NP-Completeness”, San Francisco: W.H. Freeman. ISBN 0-7167-1044-7. OCLC 4195125; 1979.
FAQ
Wat is post-quantum cryptography (PQC)?
Post-quantum cryptografie gaat over versleutelingsmethodes die ook veilig blijven als er straks krachtige kwantumcomputers bestaan. In tegenstelling tot de huidige algoritmes, die door zulke computers makkelijk te kraken zijn, maakt PQC gebruik van wiskundige problemen die zelfs voor kwantumcomputers lastig blijven.
Waarom lopen onze huidige beveiligingssystemen risico door kwantumcomputers?
De meeste openbare-sleutelmethodes, zoals RSA en elliptische-curvecryptografie, zijn gebaseerd op rekenproblemen die kwantumcomputers heel snel kunnen oplossen. Zodra die krachtige computers er echt zijn, kunnen ze daardoor de huidige beveiliging breken.
Welke PQC-methoden lijken het meest veelbelovend?
Vooral de zogeheten lattice-based cryptografie (zoals CRYSTALS-Kyber en CRYSTALS-Dilithium) en sommige code-based systemen (zoals Classic McEliece) staan bovenaan de lijst. Deze horen ook bij de algoritmes die NIST aan het standaardiseren is voor toekomstig gebruik.
Worden symmetrische algoritmes ook beïnvloed door kwantumcomputers?
In mindere mate. Kwantumcomputers kunnen brute-force aanvallen iets versnellen, maar dat los je op door de sleutels simpelweg groter te maken, bijvoorbeeld van 128 naar 256 bits. Daarmee blijft het veilig.
Wat kunnen organisaties nu al doen om zich voor te bereiden?
Begin nu al met plannen om over te stappen op PQC-algoritmes, houd de NIST-standaarden in de gaten en zorg dat je systemen flexibel genoeg zijn om snel nieuwe cryptografische oplossingen te kunnen gebruiken zodra die beschikbaar komen.


